
The first section of this note reviews the concepts of soil water movement (using Darcy’s law) under primarily saturated conditions with an emphasis on saturated hydraulic conductivity (Ks). A discussion is included on how Ks relates to permeability. The second section describes the history of the permeability classes and the transition to the current Ks classes used by the National Cooperative Soil Survey.
Darcy’s law quantitatively describes one-dimensional water flow in saturated soil and is written as:
J = –Ki Eq. 1
where J is water flux (or flow of water), K is hydraulic conductivity, and i is hydraulic gradient. The minus sign keeps K positive and maintains directional integrity; hydraulic gradient always decreases in the direction of water flow. For simplicity, the minus sign is omitted in the remaining discussion.
Darcy’s law demonstrates that flux (J) is proportional to the hydraulic gradient (i). Hydraulic conductivity (K) is the constant that defines the proportionate relationship of flux to hydraulic gradient.
The dimensions assigned to flux and hydraulic gradient determine those of saturated hydraulic conductivity. The dimensions may vary.1
Water flux (J) is defined as:
J = Q/At Eq. 2
where J is the quantity of water (Q) moving through a cross-sectional area (A) per unit of time (t) (figure 1).

Figure 1.—Water flux (J) is the quantity of water (Q) moving through a cross-sectional area (A) per unit of time (t).
Flux can be thought of as water flowing from a hose. The flux is the rate of water discharged by the hose, divided by the cross-sectional area of the hose (e.g., gal/hr in2 or in3/hr in2 = in/hr).
Flux is commonly expressed on a volume basis (e.g., m3/m2 s), which simplifies to a velocity unit (m/s). Flux, however, is not the distance water travels per unit time as the simplification suggests. The original units represent volume (quantity) discharged (i.e., collected and measured) through a cross-sectional area per unit time.
Hydraulic gradient describes the effectiveness of the driving force behind water movement and is defined as:
i = ΔH / l Eq. 3
where ΔH is the difference or change in total water potential between points in the soil (see the following discussion of soil water potential) and l is the distance between the points. For this technical note, hydraulic head represents soil water potential. The hydraulic gradient is the difference in total hydraulic head per unit distance.
Soil Water Potential
Soil water potential is the driving force behind water movement. The main
advantage of the “potential” concept is that it provides a unified measure by
which the water state can be evaluated at any time and everywhere within the
soil-plant-atmosphere continuum (Hillel, 1980).
Soil water is subject to a number of forces. These forces include gravity,
hydraulic pressure, the attraction of the soil matrix for water, the presence of
solutes, and the action of external gas pressure (Hillel, 1980). At any point in
the soil, total soil water potential is the sum of all of the contributing
forces.
For Saturated Flow:
The two primary driving forces are the submergence component of pressure head
and the gravitational head. Thus, total soil water potential, also known as
total hydraulic head (H), can be expressed as:
H = Hg+Hp
Eq. 4
where:
Hg =gravitational head, which is the vertical position of a point relative to a
selected elevation datum (e.g., see datum in figure 2). Gravitational head
equals the distance above (+) or below (-) the datum (e.g., potential head in
cm). The relative elevation difference between a point and the datum determines
gravitational head. From an energy perspective, gravitational head is the work
required to move water from the datum to its present position (e.g., Hig in
figure 2).
Hp=pressure head due to submergence. It has a zero (0) value at the surface of
the water table and increases (has a positive value) with depth below the
surface of the water table (e.g., Hip in figure 2).
Note:
Additional soil water potentials may appreciably influence water flow under
specific conditions. Most notable is the matric potential.
Hm=matric head, a pressure component attributed to soil matrix capillary and
adsorptive forces. Matric head is also called tension or suction. Matric head is
an important factor in unsaturated flow and imparts a negative (-) pressure head
value.
Other soil water potentials (e.g., osmotic, thermal, and solution) are not
discussed here.
Figure 2 illustrates the variables involved in hydraulic gradient. The figure shows a soil core encased in a cylinder to assure both a constant cross-sectional area and a one-dimensional vertical saturated flow. Total hydraulic head at both the inflow (Hi = Hig+Hip)2 and outflow (Ho = 0) are determined relative to the datum. The total head difference (ΔH = Hi -Ho) between the inflow and outflow is the driving force for water flow. The effectiveness of this driving force depends on the distance (l) between the inflow and outflow. The total head difference between inflow and outflow (ΔH) divided by the distance (l) is the hydraulic gradient i. An increase in the total head difference or a decrease in the distance (l) increases the hydraulic gradient. The result is an increase in flux or flow rate.
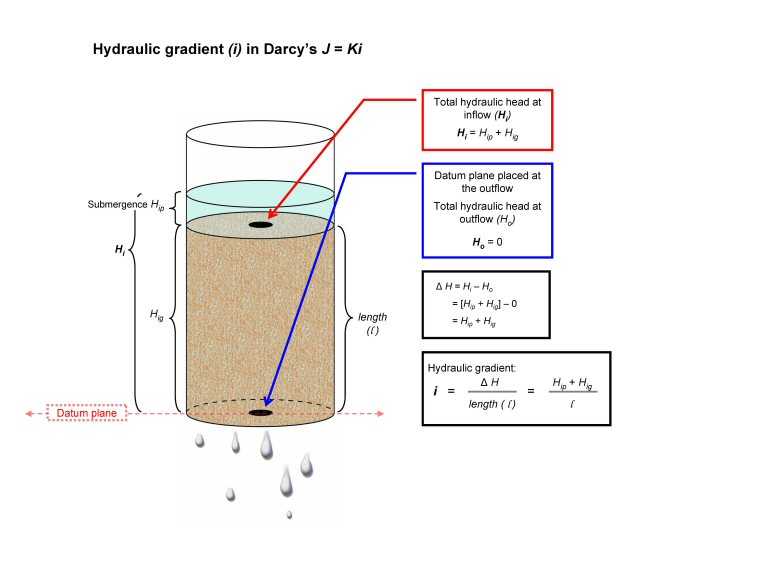
Figure 2.—Hi and Ho are the total hydraulic head at inflow and outflow, respectively. The datum plane is selected at the output, and so Ho is “0.” The difference between Ho and Hi is ∆H. For a vertical core with the datum at the bottom, the gravitational component (Hig) and the core length (l) are equal. Consequently, variations in the submergence component (Hip) can effectively regulate flux. Increasing the submergence component (Hip) increases hydraulic gradient, which in turn increases flux.
Water moves from points of higher to lower total hydraulic head regardless of whether the points are in a soil core (as in figure 2) or in a soil landscape.
Saturated hydraulic conductivity is a quantitative measure of a saturated soil's ability to transmit water when subjected to a hydraulic gradient. It can be thought of as the ease with which pores of a saturated soil permit water movement.
In Darcy’s law, saturated hydraulic conductivity is a constant (or proportionality constant) that defines the linear relationship between the two variables J and i (figure 3). It is the slope of the line (J/i) showing the relationship between flux and hydraulic gradient. Solving Darcy’s equation for K yields J/i (see equation 5). Flux represents the quantity of water moving in the direction of, and at a rate proportional to, the hydraulic gradient. If the same hydraulic gradient is applied to two soils, the soil from which the greater quantity of water is discharged (i.e., highest flux) is the more conductive (greatest flow rate). In figure 3, the sandy soil yields a higher flux (is more conductive) than the clayey soil at the same hydraulic gradient. The soil with the steeper slope (the sandy soil in figure 3) has the higher hydraulic conductivity. Hydraulic conductivity (or slope “K”) defines the proportional relationship between flux and hydraulic gradient, or in this case, of unidirectional flow in saturated soil. Saturated hydraulic conductivity (“Ks”) is a quantitative expression of the soil’s ability to transmit water under a given hydraulic gradient.
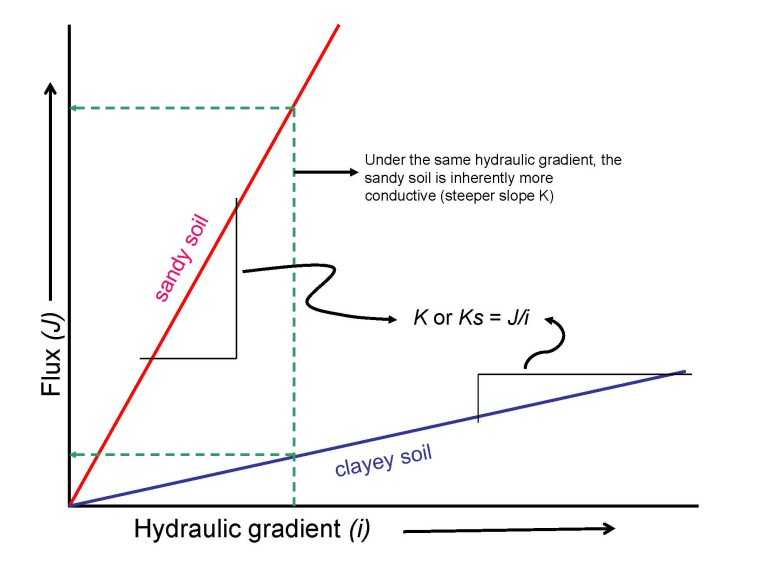
Figure 3.—A diagram showing the relationship between flux and hydraulic gradient. Hydraulic conductivity (K) is the slope that defines the relationship. The dotted lines show that at equal hydraulic gradients, soils with higher conductivity have higher flux. Figure modified from Hillel, 1980.
Saturated hydraulic conductivity is affected by both soil and fluid properties. It depends on the soil pore geometry as well as the fluid viscosity and density. The hydraulic conductivity for a given soil becomes lower when the fluid is more viscous than water.
Pore geometry and continuity within a soil or landscape vary depending on the direction of measurement. The vertical component of K can be different from the horizontal component.
In a hose, Ks is the combined effect of water viscosity, water density, and flow resistance along the perimeter, which are constant regardless of water pressure or flux.
Solving Darcy’s law for hydraulic conductivity (K) yields:
Hydraulic conductivity (or Ks) is expressed using various units. The units and dimensions depend on those that are used to measure the hydraulic gradient (mass, volume, or weight) and flux (mass or volume).3
Flux (J) is commonly expressed on a volume basis, and the units simplify to m/s. The hydraulic head difference (ΔH) is commonly expressed on a weight basis. It simplifies to centimeters of head, and the hydraulic gradient (i) becomes unitless (e.g., cm/cm). Then, Ks takes the same units as flux (m/s).
When the hydraulic gradient is unitless and the flux is expressed as a volume, then Ks has dimensions of length/time and units of velocity (e.g., m/s). Hydraulic conductivity, therefore, is easily mistaken for the rate of water movement through soil. Although hydraulic conductivity is expressed in velocity units (m/s), it is not a rate.
Flux numerically equals the hydraulic conductivity only when the hydraulic gradient is equal to 1 (i = 1 in equation 5). To equate a Ks value directly to a measured rate, the hydraulic gradient must equal one.
In summary, flux is a rate (the dependent variable in figure 3), hydraulic gradient is the driving force behind flux (the independent variable in figure 3), and hydraulic conductivity is the proportionality constant that defines the relationship between the two. Hydraulic conductivity is an important property because it can be used to calculate the corresponding flux from any hydraulic gradient.
The term “permeability” has three separate, but related, meanings:
The different meanings for permeability are not scientifically interchangeable. Indeed, the explicit meaning of the term “permeability” may not be discernable from written or verbal context alone. The first of the three meanings carries no quantitative implications, whereas the second and third have specific, quantitative applications. Confusion often arises because the meanings are overlapping. Present scientific convention avoids use of the third meaning entirely and is an important reason for using saturated hydraulic conductivity (Ks).
| Saturated Hydraulic Conductivity (Ks) | Intrinsic Permeability (k) |
|---|---|
| Temperature Dependent | Temperature independent |
| Fluid viscosity dependent | Constant regardless of fluid viscosity, unless the liquid itself changes soil structure |
| Changes with change in structure | Changes with change in structure |
| Dimensions depend on flux and gradient; time is a component. | Dimensions are length2 (cm2), which is a unit of area; time is not a component. |
The idea of qualitatively describing water movement was first introduced in the Soil Conservation Survey Handbook (Norton, 1939). Two permeability classes were suggested—favorable and unfavorable. The handbook, however, neither defined the terms nor offered guidance for placing a soil into classes.
To provide national consistency in defining permeability classes in soil surveys, Uhland and O'Neal (1951) evaluated percolation rates of about 900 soils. They defined “permeability” classes by distributing the percolation data equally among seven tentative classes (table 2). Along with percolation data, they also studied 14 soil morphologic characteristics that affect water movement and that could be used to make predictions regarding permeability class. Because of management effects on surface horizons, they confined their study to horizons below the surface layer. These classes were published in the 1951 Soil Survey Manual (Soil Survey Staff, 1951).
Mason et al. (1957) statistically analyzed Uhland and O'Neal's data. They concluded that it was overly optimistic that one could correctly place a given soil into one of seven permeability classes on the basis of percolation rates of five core samples taken at one site (the probability of being correct was 30%). A reasonable degree of reliability could be achieved if either more sites per soil were sampled or fewer classes were used. The study suggested that a 95% probability of making a correct placement could occur by using three to five permeability classes. In 1963, the NCSS National Soil Moisture Committee proposed a class/subclass “choice schema” with five to seven classes (table 2) (Soil Survey Division, 1997). The proposal was provisionally accepted, pending the outcome of discussions comparing auger-hole percolation tests with the Uhland core method and pending additional information on critical limits.
By the 1960s, most field studies for determining septic tank absorption field suitability utilized auger-hole percolation test methodologies. Auger-hole methods measure water flowing in multiple directions under a variable hydraulic gradient. The more controlled Uhland core method measures one-dimensional percolation rates (vertical downward flow) in the laboratory. Because the original permeability classes were devised using flow rates from the Uhland core method, the general concern was whether or not the two methods would give similar values and thus ensure consistent class placement. Studies with the auger-hole method by the Soil Survey Lab, Beltsville, Maryland, reported 100-fold differences in flow rates due to the length of time allowed for pre-wetting alone (Franzmeier et al., 1964). Franzmeier was not comfortable using results from the auger-hole method for class placement (Soil Survey Division, 1997). In 1969, the final recommendation from the NCSS National Soil Moisture Committee was that the Uhland core method should be used for saturated flow (i.e., permeability class placement) and the auger-hole method should be used for drain field suitability (Soil Survey Division, 1997).
In 1969, the NCSS National Soil Moisture Committee recommended that the term:
“...saturated hydraulic conductivity be used for data expressed as a velocity and obtained by analysis using Darcy's law on saturated cores.”
The committee further stated:
“The permeability classes in the Soil Survey Manual may be renamed hydraulic conductivity classes with no change in class limits. Although the data on which classes are based were not analyzed by Darcy's law, it turns out that since the head and length of the core were nearly equal, they may be considered hydraulic conductivity values.”
At the 1971 NCSS Conference, in a provisional outline to revise the 1951 Soil Survey Manual, five classes of saturated hydraulic conductivity were proposed. The classes included a 10-fold separation in class limits; that is, the limits of each class exceeded the limits of the previous class by a factor of 10 (see table 2). The proposed reduction from seven to five classes might be credited to Mason's (1957) findings regarding the low probability of correctly placing a soil in the original permeability class structure.
Also in 1971, the same year that the five saturated hydraulic conductivity classes were proposed, new permeability classes were officially adopted in the Guide for Interpreting Engineering Uses of Soils (USDA–SCS, 1971). Although the number of classes was unchanged (still seven), a 3-fold separation in class limits was adopted (i.e., 0.06–0.2, 0.2–0.6, 0.6–2.0, etc.)
The soil interpretations record form (SCS-SOI-5), informally called the Form–5, was the first nationally approved data-entry form for building soil survey databases. It was devised in 1970–1971 and became fully operational in 1972 (Harvey Terpstra, Iowa State University Statistical Laboratory, Ames, Iowa, personal communication). Classes from the 1971 Guide for Making and Interpreting Engineering Uses of Soils were used to enter estimates for permeability (<0.06, 0.06–0.2, 0.2–0.6, 0.6–2.0, 2.0–6.0, 6–20, and >20 in/hr). The instructions for the form specified that, for each soil layer, the limits for a class, such as 0.2-0.6 or 0.6-2.0, were to be entered or the limits for a combination of classes, such as 0.2-2.0, were to be entered.
Also during the 1970s, national soils memoranda, which provided detailed instructions for making and interpreting soil surveys, were progressively cancelled and replaced by sections of the National Soils Handbook (later renamed the National Soil Survey Handbook). It was therefore appropriate for the National Soils Handbook to contain instructions similar to those in the memoranda. Thus, the same advice for entering permeability classes on Form–5 was given in the National Soils Handbook as was in the memoranda.
When the Soil Survey Division converted its previous database to the National Soil Information System (NASIS) in 1994, saturated hydraulic conductivity replaced permeability. Only the name was changed at this time. The values from the previous database were imported directly into NASIS without modification.
During the late 1970s and early 1980s, Dr. Ron Paetzold, then with the Soil Survey Laboratory, Beltsville, Maryland, conducted an exhaustive review of the literature on soil values of saturated hydraulic conductivity for revising the Soil Survey Manual. He arrayed the published data and constructed six saturated hydraulic conductivity classes with a 10-fold separation (e.g., 0.01–.1, 0.1–1, 1–10, etc.) in SI units of μm/s.
In 1981, chapter 4, “Examination and Description of Soils in the Field," of the revised Soil Survey Manual (then in progress) was officially adopted and formally transmitted by national directive. The national directive established Paetzold's classes for saturated hydraulic conductivity and invalidated further use of permeability classes. Reducing the number of classes by increasing the separation of class limits from 3-fold to 10-fold considerably improved the likelihood of correctly estimating class placement. The 1981 national directive stated:
“...the Manual should not be supplemented with state or Technical Service Center directives...”
Paetzold prepared the discussion of saturated hydraulic conductivity for the 1993 Soil Survey Manual (Soil Survey Division Staff, 1993), in which the 10-fold class set was retained. The Soil Survey Division apparently did not place a strong subsequent emphasis on the matter, however, because some states continued to use the permeability classes from the 1971 Guide for Interpreting Engineering Uses of Soils.
The 1983 version of the National Soils Handbook (Soil Survey Staff, 1983) published classes for both saturated hydraulic conductivity and permeability. In 1993, the National Soil Survey Handbook (NSSH) dropped the saturated hydraulic conductivity classes, retained permeability classes, and added an eighth class (see column “1996” in table 2). In addition, index surface runoff, originally designed with saturated hydraulic conductivity classes for the Soil Survey Manual, was modified with permeability classes in the NSSH. This attempt at standardization was less than satisfactory because class limits in the six saturated hydraulic conductivity classes could not be directly converted to the eight permeability classes. The result was differing criteria between the Soil Survey Manual and the NSSH for determining surface runoff indices and differing terminology and classes for soil water movement (i.e., saturated hydraulic conductivity in the 1993 Soil Survey Manual and permeability in the NSSH).
To resolve the saturated hydraulic conductivity issue, the Soil Survey Division in 2003 again confirmed saturated hydraulic conductivity classes as the standard for communicating water movement in national cooperative soil surveys. This decision is a reiteration of all the recommendations from NCSS regional and national committees beginning in the 1960s and culminating, by national directive, in the 1981 distribution of saturated hydraulic conductivity classes in chapter 4 of the revised Soil Survey Manual. Permeability classes and most references to permeability have been removed from the NSSH and replaced with the saturated hydraulic conductivity classes of the 1993 Soil Survey Manual. The NSSH adopted the index surface runoff guide from the Soil Survey Manual, without reference to classes, as well as the guidelines for estimating saturated hydraulic conductivity. Except for the PEDON side of NASIS, saturated hydraulic conductivity (not permeability) is the current standard data-entry term, and so no revisions are necessary4. In a future release of PEDON, appropriate revisions to data fields and choice lists will be made.
[Values are upper class values, except for the highest class.]
| 1951 | 1963 | 1971 | 1971 | 1981 | 1983 | 1996 | 2003 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Permeability classes | Ks classes first proposed | Permeability classes officially revised | Ks officially adopted | NSSH5 includes both Ks and permeability classes | NSSH drops Ks includes permeability only (8 classes) | NSSH drops permeability, includes Ks only (6 classes) | ||||||
| Uhland & O'Neal, Soil Survey Manual | NCSS6 Conference proposal | NCSS Conference | NCSS Conference (Guide for Interpreting Engineering Uses of Soils adopted) | NRCS Soil Survey Division issues chapter 4 of the revised Soil Survey Manual |
||||||||
| in/hr | in/hr | cm/day | (in/hr) | μm/s | in/hr | in/hr | μm/s | Six Ks classes (1981) | Seven permeability classes (1971) | in/hr | μm/s | |
| Classes | Sub-classes | < 1 | < (.016) | < .12 | < .001417 | < 0.01 | < 0.00157 | < 0.01 | ||||
| <0.05 | < 0.2 | < 0.063 | 10 | (0.16) | 1.16 | < 0.06 | .01417 | 0.1 | 0.06 | 0.1 | ||
| 0.20 | 0.063 to 0.2 | 0.2 | .1417 | 1.0 | 0.2 | 1.0 | ||||||
| 0.80 | 0.63 | 0.63 | 100 | (1.6) | 11.6 | 0.6 | 1.417 | 10.0 | 0.6 | 10.0 | ||
| 2.50 | 2.00 | 2.00 | 2.0 | 2.0 | ||||||||
| 5.00 | 6.3 | 6.3 | 1000 | (16) | 116 | 6.0 | 14.17 | 100 | 6.0 | 100 | ||
| 10.00 | ≥ 6.3 | 6.3 to 20.0 | 20.0 | 20.0 | ≥ 100 | |||||||
| ≥ 10.00 | ≥ 20.0 | ≥ 1000 | ≥ (16) | ≥ 116 | ≥ 20.0 | ≥ 14.17 | ≥ 100 | 100 | ||||
1. Dimensions are length, time, and
mass. Likewise, length2=area and length3=volume.
2. Total water potential can be expressed on the basis of volume, mass, or
weight. Weight is the most common basis and is referred to as “hydraulic head,”
the dimension of which simplifies to length (e.g., cm). Hydraulic head expressed
as length is more straightforward and easier to comprehend than water potentials
expressed as a volume (e.g., cm2/s2) or a mass basis (e.g., g/cm s2).
3. When both flux and potential are expressed as a mass, the Ks units are
kg-s/m3. If both are expressed on a volume basis, the Ks units are m3s/kg. If
flux is expressed as mass and potential is expressed as hydraulic head, the Ks
units are kg/m2s. If flux is expressed as a volume, and potential expressed as
hydraulic head, Ks has length/time dimensions and the units are m/s.
4. Although many local NASIS reports probably still output “permeability”
classes and terms.
5. NSSH—National Soil Survey Handbook
6. NCSS—National Cooperative Soil Survey
7. The permeability class of < 0.0015 in/hr approximates the limit of 1 foot/
year used by engineers from the EPA and NRCS for impermeable conditions for
manure holding ponds.
The contact for this technical note is the National Leader for Soil Classification and Standards, National Soil Survey Center, Lincoln, NE.